DreamBox Learning Math for Indiana
DreamBox is proven to increase math growth. This K-8 online math program supplements core instruction in the classroom and at home. It dynamically adapts to the learner, providing personalized instruction. DreamBox lessons are available in English and Spanish and aligned to Indiana state math standards.
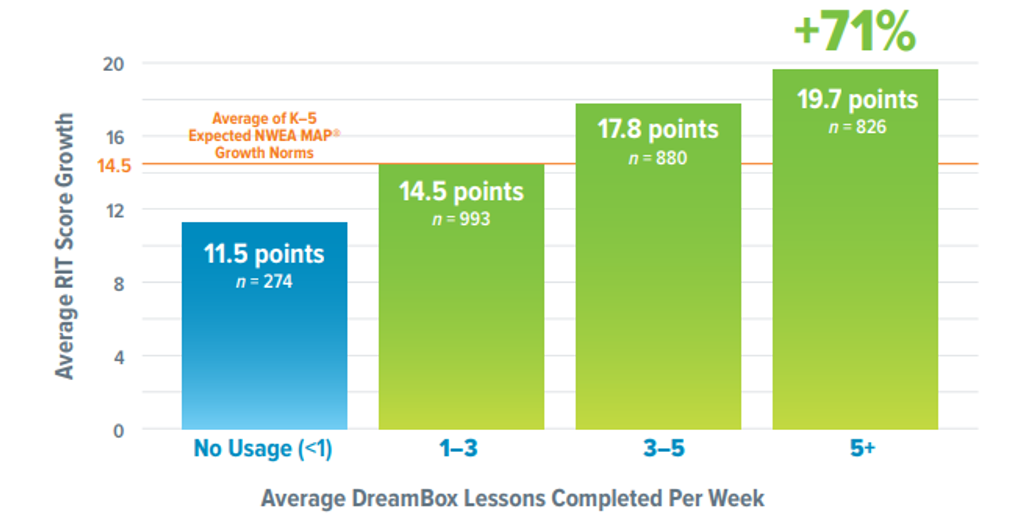
DreamBox Learning Helps Improve NWEA® MAP ® Growth by 71%
Teachers know and are able to talk about their students as mathematicians with the use of formative data from DreamBox as well as use this information to scaffold and personalize instruction to help ensure growth of all students.

Dr. Lynn Simmers - Assistant Superintendent
Southwest Allen County Schools

Social-Emotional Learning
In DreamBox, students...

Educator Dashboard
In DreamBox, educators can...

Case Study
Fort Wayne Community Schools
We use DreamBox to drive our one-on-one instruction and lesson plans so we can focus on kids who have huge gaps in their learning. We are able to see where each student is in their learning and where they need additional support, which makes our intervention a lot more powerful for our students.

Anna Wiley
Math Intervention Teacher, DeKalb Central School District
Interested?
Contact Us To Learn More
View Standards
Aligns to Indiana Academic Standards for Mathematics (IASM)
Give DreamBox a Spin
Ready to see if DreamBox is right for you and your students?









