Try DreamBox Math Lessons
DreamBox offers over 2,000 lessons with millions of paths through the curriculum. To engage students exactly where they are, it adjusts in real-time, adapting hints, level of difficulty, pace, and sequence.
Explore Grade Level Environments
Choose a Grade and Lesson to Sample
Kindergarten
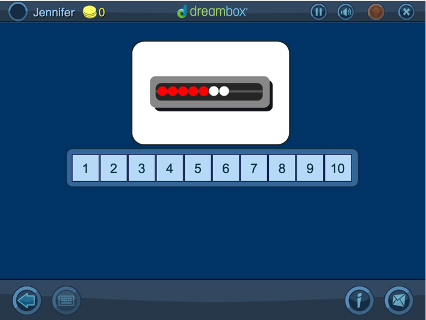
Recognizing Quantity on a Quick Image: Up to 10 on the Math Rack
Using the familiar tool of a math rack to display various quantities from 1-10, students are briefly shown an image of an amount of beads and then asked to choose the number they saw on the numberline. “Quick Images” are an effective strategy to help students learn to conceptualize a number in a variety of ways. This helps students to use numbers flexibly, which is an important facet of number sense.
Kindergarten
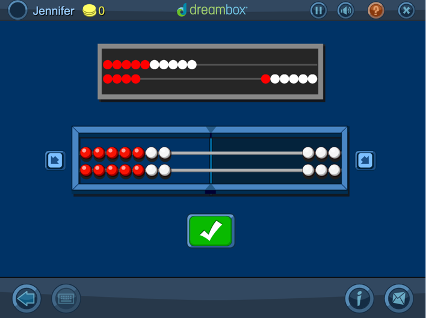
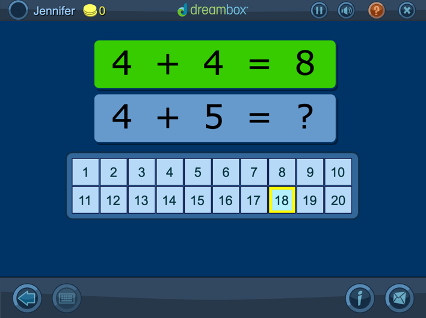
Representing Numbers to 20 in Two Different Ways on a Math Rack
With a mathrack virtual manipulative, students learn that you can build the same number in several different ways, e.g. 10+3 = 7+6. Students can use a variety of strategies to solve these problems, including the commutative property (10+4 = 4+10), doubles or near doubles (10+4 = 7+7), and more.
Kindergarten
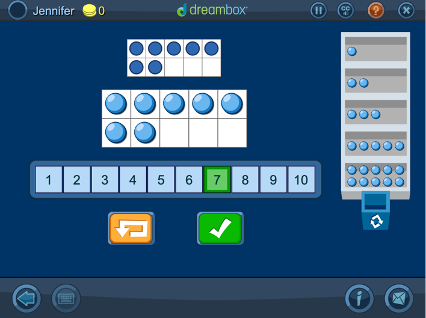
Representing Numbers to 10 on a Ten Frame and Identifying the Numeral
Virtual tools push students beyond counting by ones to using groups of 2, 3, 5 and 10. After successfully building numbers, students are given more “restrictions,” like building numbers from a number other than 0.
First Grade
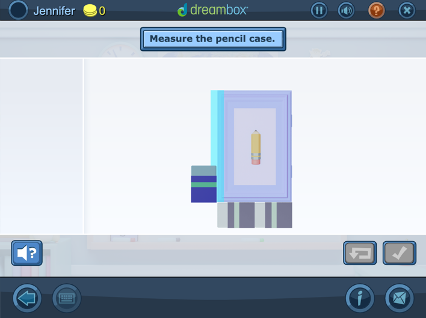
Using Tools to Explore the Measurement of Object Dimensions
Students’ exploration of measurement continues as they begin to measure the different dimensions of objects using non-standard tools. Using common classroom items as digital manipulatives to calculate the lengths and widths of objects, students also begin to understand that tools need to be rotated depending on the dimension being measured and that different sized tools are going to result in different measurements of the length and width.
Second Grade
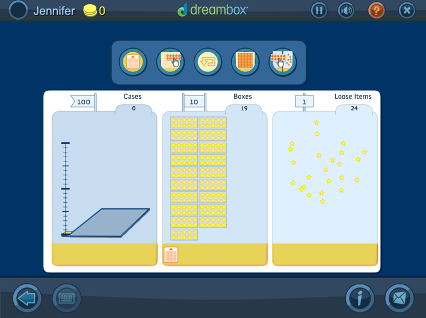
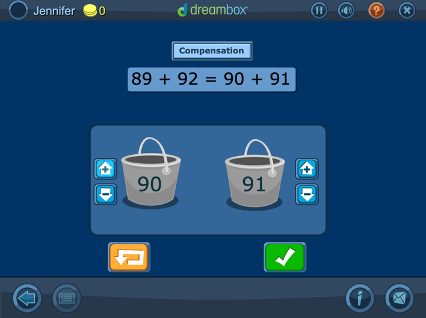
Addition with a Compensation Strategy Using a Manipulative with Counters
Turn hard problems into “friendlier” problems by making one of the addends a multiple of 10. Students start with smaller 2-digit addends, and when they’re ready they use 3-digit addends. It’s an efficient mental math strategy.
Second Grade
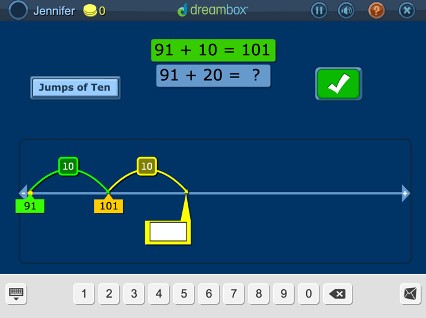
Associated Addition Equations: Adding a Multiple of 10 and Near Multiple of 10 on the Number Line
Students visualize making jumps on a number line and use a variety of strategies for both addition and subtraction. Strategies include “Making Jumps of 10” (e.g. 79+33 = 79+10+10+10+3) and “Using Landmark Numbers” (e.g. 79+33 = 79+1+20+10+2).

Third Grade
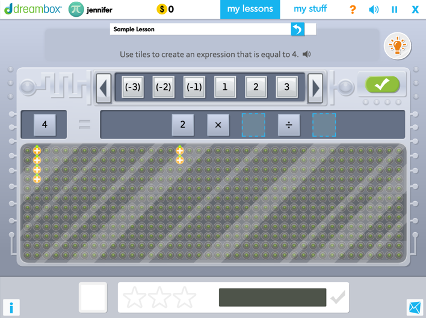
Representing Products to 144 by Partial Products and Arrays
In a series of activities, a given rectangle is covered using smaller rectangles. As grid lines are removed, students work with open arrays. As rectangles are moved, students explore ideas in multiplication: distributive, associative, and commutative properties.

Third Grade
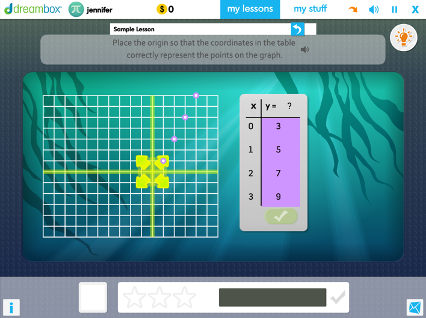
Marking and Labeling Fractions Between 0 and 2 on a Number Line
A number line representation ensures students can compare and order fractions apart from any specific part-whole context. Students use landmark fractions and numbers to place fractions on the number line from 0 to 1 and from 0 to 2.
Fourth Grade
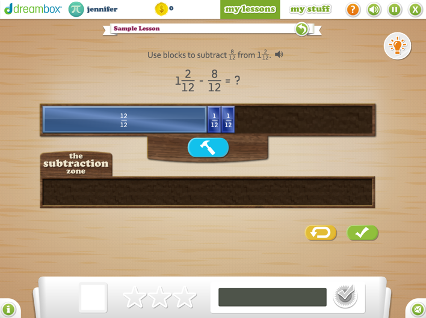
Subtracting Fractions of Like Denominator Using Number Blocks
This lesson helps students think conceptually, not procedurally, about subtracting fractions by using the “removal” or “take away” strategy. This enables skill of subtracting mixed numbers and improper fractions fluently, mentally, and easily.
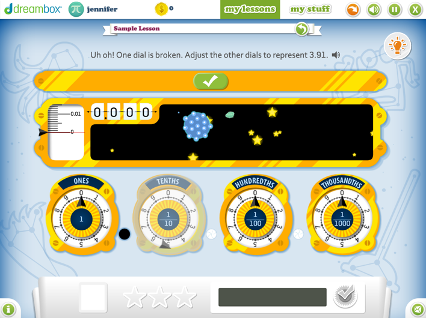
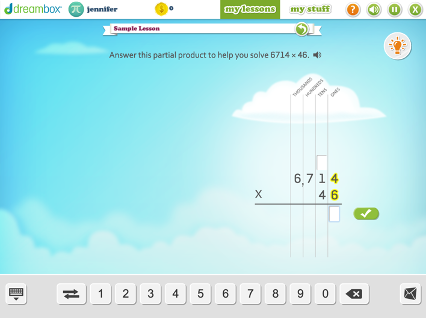
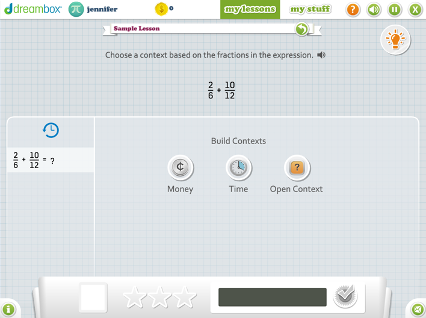
Fifth Grade
Adding Fractions with any Unlike Denominators Using Money, Time, or an Open Context on a Bar Model
Students add fractions with unlike denominators using money, time, or an open bar model as context. With these contexts, they are able to use familiar contexts and visuals to help them find a common multiple of the denominators in order to add them together.
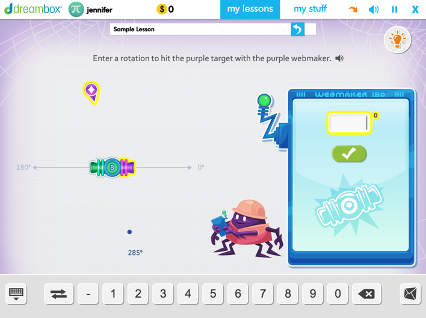
Sixth Grade
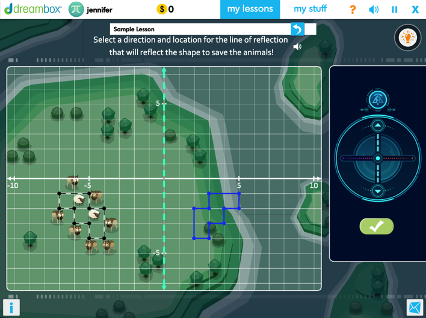
Using 180 Degree Relationships to Determine Angle Measurement to a Given Target
Students deepen understanding of angle measurement and rotation while fluently reasoning about and using supplementary and vertical angle relationships. Students use deductive reasoning to make rotations, aim for targets, and determine angle measurements.
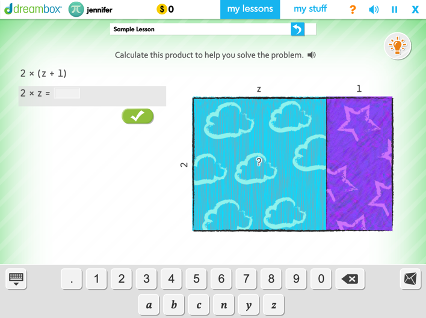
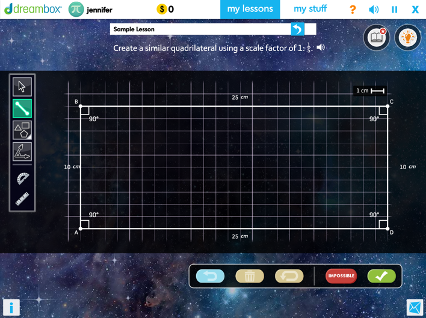
Seventh Grade
Constructing Similar Polygons Using Fractional and Whole Number Scale Factors
Students are given a shape with marked angles and side lengths, then asked to create a new shape using scale factor by constructing different types of triangles, quadrilaterals, regular polygons, and scaled polygons.