Math Learning in the Zone of Proximal Development

Taking the different learning pace, habits of mind, and prior knowledge of individual students into account in mathematics can be challenging. Math educators know that unless students are challenged by and actively engaged in the course material, students will quickly lose attention. If the challenge is too great, students might simply give up. By understanding the concept of a zone of proximal development and how to connect with learners at different developmental points, teachers can plan a more strategic approach to group and individual instruction.

Sourced from http://www.instructionaldesign.org/theories/social-development.html

What is the zone of proximal development?

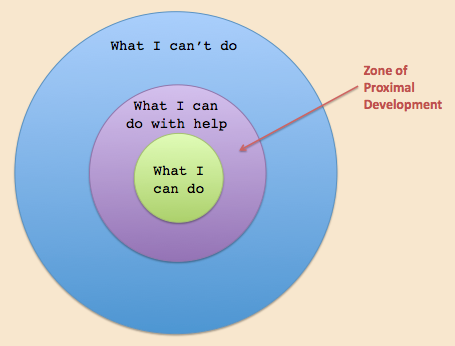
The zone of proximal development (ZPD), often referred to as the optimal learning zone, is a concept developed by social cognitive theorist and psychologist Lev Vygotsky. It is the gap between what a student knows and what he or she can achieve given appropriate and pedagogically sound guidance and educational support.

Each student is uniquely in multiple and different zones depending on the content and an individual’s prior knowledge and interests. Learning that occurs within the ZPD should neither be too easy nor too difficult. It needs to be just enough of a challenge to help the student deepen conceptual understanding and develop new skills that build upon the student’s existing knowledge and understanding.

ZPD in the math classroom

Because the concept of ZPD involves connecting unlearned material to what is familiar, teachers play a pivotal role in the application of ZPD in the classroom. They provide appropriate scaffolding—strategic social interactions, learning experiences, and instruction based on a student’s past performance, intuition, and current thinking—that guide effective learning and development.

Scaffolds facilitate a student’s ability to make sense of new situations, build on prior knowledge, and transfer learning. There are many ways to scaffold to improve learning. In the math educational setting, scaffolds may include manipulatives, games, models, cues, prompts, hints, partial solutions, think-aloud modeling, or using contextual problems based on a student’s interests. Scaffolds should engage students in sense-making and critical thinking.

Intelligent Adaptive Learning TM software and the ZPD

Advances in adaptive learning systems and platforms that empower pedagogically sound feedback for students can be used in blended learning environments for greater personalization.   The ability of students to track their own learning progress means that they can develop valuable self-monitoring skills while engaged and empowered in their personal learning progress.

Pedagogically and research-based intelligent adaptive learning technology supports students as they work in an appropriate ZPD. Because adaptation happens within and between lessons in real-time, intelligent adaptive learning systems provide the right next lesson, at the right level of difficulty, at the right time.

By keeping the challenge appropriate, the learner is empowered to be a mathematical ‘thinker’ and ‘doer’ — someone who strategically solves problems in ways they can apply in school and in their real life experience.*

*Sourced from DreamBox http://www.dreambox.com/why-dreambox