What Are Ratios?
Learn how ratios help you compare quantities in real life.
Author
Tess Loucka
Published:
October 2025
Key takeaways
- • Ratios are a comparison tool used to visualize differences between quantities.
- • There are two types of ratios: part-to-part ratios and part-to-whole ratios.
- • You can expand or simplify ratios the same way you would expand or simplify fractions—using multiplication and division.
Ratios are one of the greatest comparison tools in math. Yet many people struggle to explain what ratios really are!
In the simplest of terms, a ratio is a comparison of two quantities. Most students know how to make greater-than or less-than statements, such as “This number is greater than that number” or “There is less water in this cup than that cup.”
Ratios take those statements further, placing them within a broader context and creating space for further calculations.
And, like all math, ratios are not just a tool for the classroom. Outside of school, students can apply their knowledge of ratios to perform various tasks, including reading distances on maps, comparing the currencies of different countries, and adjusting recipes while maintaining proper ingredient measurements.
So, ratios come in handy whether you’re out in the real world or sitting in a classroom taking a math test.
That being said, let’s talk about what ratios are, how to calculate and simplify them, and how you can use them in your daily life.
What is a ratio?
What does ratio mean, and what are ratios in math?
A ratio is a comparison between groups of things or quantities, written as two numbers separated by a colon.
For example, 6:8.
What’s special about ratios is that they aren’t just a comparison, but a rule. The ratio 6:8, read as “six to eight,” says that for every 6 objects in the first group, there will always be 8 objects in the second group.
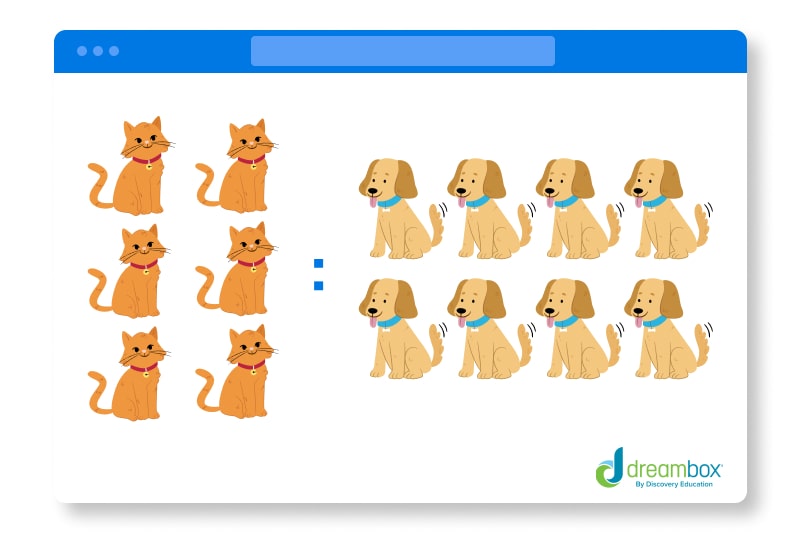
Using the image above, we could say there are six cats to eight dogs. That means, for every six cats, there will always be eight dogs.
If the number of cats were to grow or shrink, the number of dogs must also grow or shrink, in accordance with the ratio. This remains true if the number of dogs were to change—the number of cats would have to change accordingly.
In accordance with the ratio 6 cats : 8 dogs, if there are 12 cats, how many dogs should there be?
Think about the ratio! The number of cats changed from 6 to 12. In other words, the number of cats doubled. Therefore, the number of dogs must double as well.
If there are 12 cats, there should be 16 dogs, making the ratio of cats to dogs 12:16.
Now, what if the number of cats were to be halved?
Since the original number of cats was 6, and 6 ÷ 2 = 3, how can we complete the ratio?
If there are 3 cats, there should be 4 dogs, making the ratio of cats to dogs 3:4.
We now have three ratios: 6:8, 12:16, and 3:4. While they look different from each other, they all demonstrate the same comparison rule.
Types of Ratios
There are two types of ratios:
- part-to-part ratios
- part-to-whole ratios.
Part-to-part ratios compare two parts of a whole, while part-to-whole ratios compare (can you guess?) one part to the whole that encompasses it.
Let’s look at an example.
The ratio of red slices to blue slices is 2:3. This is a part-to-part ratio.
The ratio of red slices to total slices is 2:8, which can be simplified to 1:4. This is a part-to-whole ratio.
Table of contents
What is the Ratio Formula
There is no official ratio formula. What you do have to remember about ratios, though, is how they are notated.
Ratios are made up of two numbers separated by a colon.
For example, 3:5 is a ratio and can be read as “three to five.”
14:3 is a ratio too and can be read as “fourteen to three.”
1,478:1 is also a ratio and is read as “one thousand four hundred seventy-eight to one.”
The first number in a ratio is called the antecedent, while the second number is called the consequent.
Ratios may also be formatted as fractions, such as 3/5, 14/3, and 1,478/1.
Formatting ratios as fractions helps to demonstrate that you can divide the antecedent by the consequent to simplify ratios to a unit of 1.
Simplifying Ratios to a Unit of 1
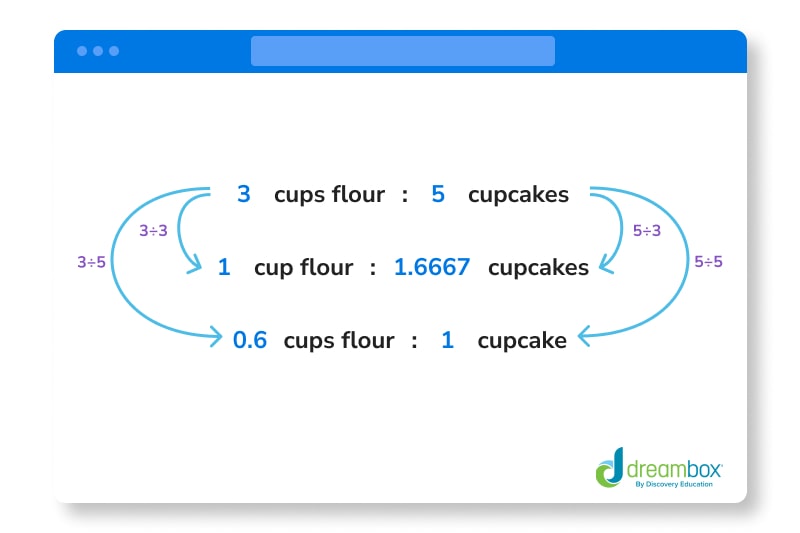
If a baker uses 3 cups of flour to bake 5 cupcakes, the ratio of flour to cupcakes is 3:5.
If we divide 3 by 5, we get 3 ÷ 5 = 0.6. Therefore, the baker uses 0.6 cups of flour for every 1 cupcake.
If we divide 5 by 3, we get 5 ÷ 3 = 1.6667. Therefore, the baker uses 1 cup of flour for every 1.6667 cupcakes.
If a baker uses 3 cups of flour to bake 5 cupcakes, the ratio of flour to cupcakes is 3:5.
If we divide 3 by 5, we get 3 ÷ 5 = 0.6. Therefore, the baker uses 0.6 cups of flour for every 1 cupcake.
If we divide 5 by 3, we get 5 ÷ 3 = 1.6667. Therefore, the baker uses 1 cup of flour for every 1.6667 cupcakes.
How to calculate Ratios
Learning how to calculate ratio problems is not as hard as it may seem. It all starts with knowing how to find ratio data.
Consider the following:
A classroom has 15 male students and 20 female students. Find the ratio of male students to female students.
To answer this problem, you need to create a ratio that can be read as “X male students to Y female students.” That means the number of male students in the class should come first. It will be the antecedent.
The number of female students should come second—the consequent.
This is a part-to-part ratio and can be written as 15:20, or 15/20.
Now, find the ratio of female students to total students in the classroom.
The number of female students will be the antecedent and the total students will be the consequent. To calculate the total students in the classroom, just add 15 to 20 to get 15 + 20 = 35.
This is a part-to-whole ratio and can be written as 20:35 or 20/35. No further calculations have to be made, unless you are asked to simplify the ratio.
How to Simplify Ratios?
Not every ratio can be simplified, but if it can, teachers usually require students to do so.
Simplifying a ratio is the same as simplifying a fraction. Just divide the two numbers evenly until one or both numbers cannot be made any simpler, more compact, or easy to use.
Let’s look at the ratio 15:20.
First of all, can this ratio be simplified?
Since 15 and 20 are both composite numbers, meaning they have numerous factors, 15:20 can be simplified.
Next, by what factor should we simplify this ratio?
The numbers 15 and 20 are both divisible by the factor of 5. So, let’s divide both numbers by 5.
15:20 = 15/20 = 15 ÷ 5 / 20 ÷ 5 = ¾
Therefore, 15:20 can be simplified to 3:4.
Ratios in Real Life
Ratios don’t just exist in the classroom; ratios are a tool used in many areas of life, from cartography and chemistry to baking!
Take a look at the simple map below.
Notice the ratio in the corner?
This ratio tells us that the distance of 1 centimeter on the map is equivalent to 25 miles in real life. This informs us of the map’s scale and makes large measurements possible.
What about this model airplane?
This real-life object also uses ratios. The ratio on the box of this model airplane is 1:32. That means, the model airplane is 32 times smaller than the real airplane the model is based on.
We use ratios in cooking and baking, too. For instance, you can use a ratio of 5:3 when baking bread from scratch. Instead of using a recipe, you can remember the ratio 5:3, which means for every 5 parts of flour, add 3 parts water.
Accordingly, if you use 15 grams of flour, make sure to use 9 grams of water to maintain the 5:3 ratio.
Examples of Ratios
If you’re still feeling shaky about what ratios are and how they can be used, here are a few more ratio examples.
- The ratio of lemon juice to water in a lemonade recipe is 1 cup to 7 cups, which can be written as 1:7 or 1/7.
- In a gym class at school, there is 1 soccer ball assigned to every group of 4 students, which can be written as 1:4 or ¼.
- The ratio of 5 apples in a fruit bowl with a total of 15 fruits in it is 5:15, which can be simplified to 1:3 or ⅓.
- In a group of 10 children and 20 adults, the ratio of children to adults is 10:20, which can be simplified to 1:2 or ½.
You can visit math apps or online resources for more examples of ratios if the concept is still confusing to you. Ratios can seem abstract to many students, so don’t feel discouraged if you aren’t confident yet.
Practice makes perfect. Try the following practice problems to test your knowledge.
Ratio Practice Problems
FAQs about Ratios
A ratio is a numerical representation of the relationship between two quantities.
An example of a ratio is 1:2, 4/15, or 150 to 2345. Ratios are simply two numbers separated by a colon or the word “to,” or written as a fraction.
A ratio is a comparison between two quantities.
Ratios can be complex, so use plenty of real-life examples, visuals, and simple practice questions to illustrate the concept effectively. Guide them through the answers until they can solve the questions independently.
About the Author
Tess Loucka
Tess Loucka discovered her passion for writing in high school and has not stopped writing since. Combined with her love of numbers, she became a math and English tutor, focusing on middle- and high-school-level topics. Since graduating from Hunter College, her goal has been to use her writing to spread knowledge and the joy of learning to readers of all ages.