All About Parallelograms
Learn all about parallelograms: the different types, formulas and examples.
Author
Katie Wickliff
Published:
May 2025
Key takeaways
- • A parallelogram is a four sided shape with opposite sides that are equal and parallel.
- • Squares, rhombuses, and rectangles are types of parallelograms.
- • Calculating the area and perimeter of parallelograms has many useful, “real world” applications.
In the early elementary years, students spend a lot of time learning to recognize and name simple shapes. By around the 3rd or 4th grade, they’re usually ready to build on their knowledge and explore more complex concepts, like parallelograms. At this stage, students learn how to identify and classify parallelograms as a type of quadrilateral. In this article, we’ll cover the different types of parallelograms, their key features, and the properties that make them unique. Since students will eventually need to calculate the area and perimeter of parallelograms, we’ve provided the formulas here. Plus, this helpful guide offers plenty of suggestions to help your kids work with parallelograms and feel confident about geometry!
What is a parallelogram?
A parallelogram is a four-sided shape with opposite sides that both run parallel and are equal in length. “Running parallel” means that the sides will never cross, no matter how long they are. The opposite angles of a parallelogram are also equal.
Table of contents
Types of parallelograms
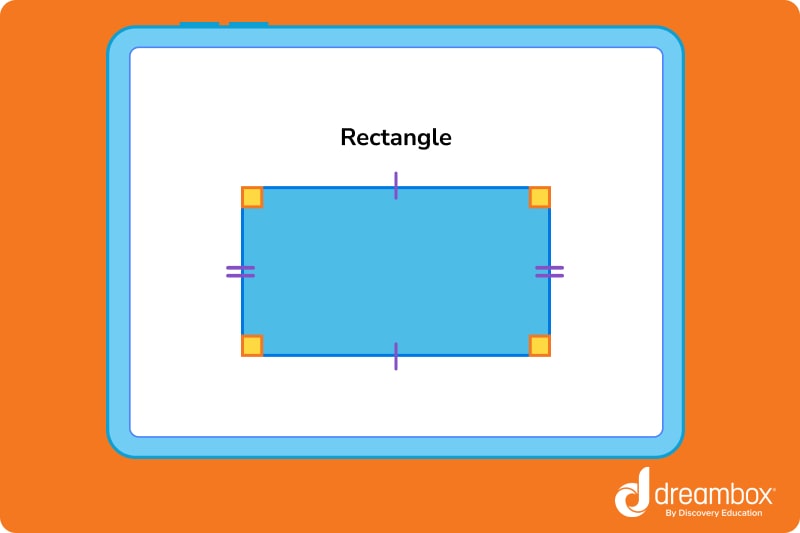
Rectangle
A rectangle is a quadrilateral (4-sided shape) where all the angles are right angles. This means that each corner measures exactly 90°. The top and bottom of a rectangle are the same length, and the two sides are also the same length.
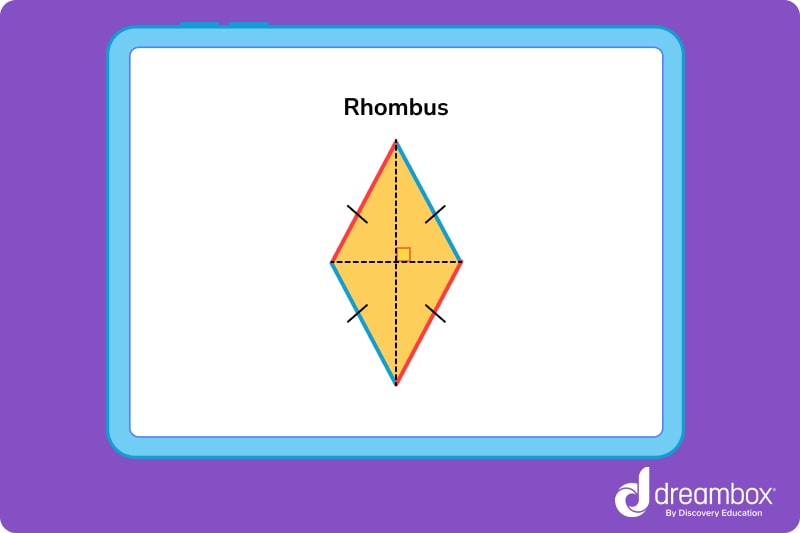
Rhombus
A rhombus is a quadrilateral where all sides are the same length, and the opposite sides are parallel. The two diagonals cross at a right angle, making 90° angles wherever they meet.
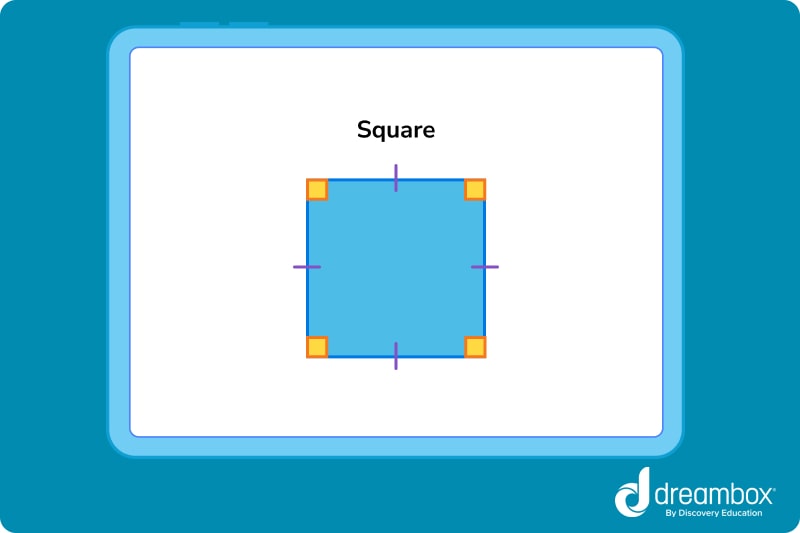
Square
Differences between parallelogram types
Key properties of parallelograms
All parallelograms have several different properties that set them apart from other shapes. These are:
Opposite sides are parallel and equal in length
The sides across from one another are equal in length. The top and bottom sides run in the same direction and never meet, and the left and right sides do the same.
Opposite angles are equal
The corners across from each other always have the same angle.
Consecutive angles add up to 180°
The angles next to each other always add up to a straight line. So, if one angle measures 100°, the other would measure 80°.
Diagonals bisect each other
The lines drawn from corner to corner cross right in the middle and cut each other into equal halves. They are not necessarily equal in length.
Parallelogram formulas: area and perimeter
Area of a parallelogram
To calculate the area of a parallelogram, first understand these definitions:
Base: the length of one side along the bottom
Height: the vertical distance from the base to the other side
Then use this formula:
Area = base x height
For example, the base of a figure is 6 inches and the height is 3 inches.
What is the area?
Area = 6 x 3
Area = 18 square inches
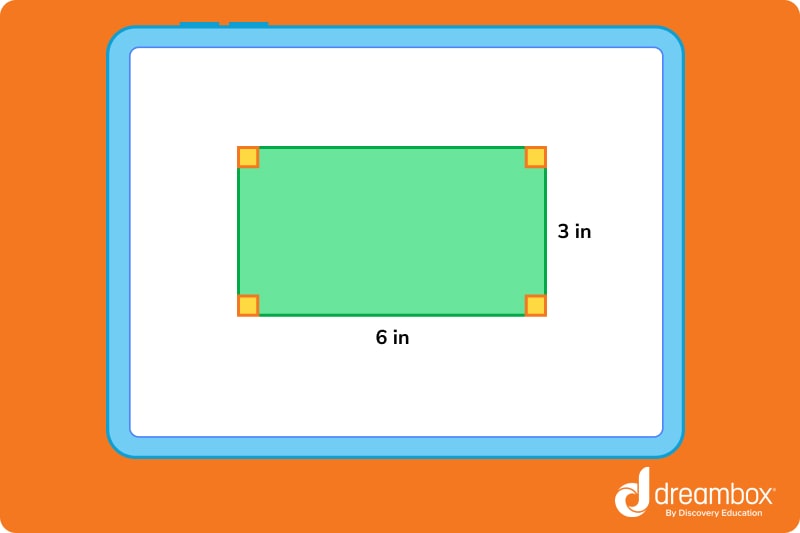
The area of parallelograms is measured in square units because it tells us how much surface space the shape covers.
Perimeter of a parallelogram
To find the perimeter (total distance around a shape), you add up the lengths of all four sides. But since opposite sides of a parallelogram are equal, you can just add the length of one pair of sides and then multiply by two.
To calculate the perimeter of a parallelogram, use this formula:
Perimeter = 2 × (length of one side + length of adjacent side)
Example:
If a size measures 7 inches and the side next to it measures 4 inches, what is the perimeter?
2 x (7 + 4)
2 x 11 = 22 inches
Applications of perimeter in real life
If your student ever wonders when they’ll actually use math in everyday life, measuring perimeter is a great example! Here are just a few everyday situations that rely on measuring perimeter.
Real-life examples of parallelograms
Our world is full of parallelograms! Here are a few examples that kids can easily spot, helping connect geometry to the real world.
Playing cards: the deck of cards is rectangular, and the diamond cards form parallelograms
Electronic screens: usually rectangles, another type of parallelogram
Playground slides: the side view often forms a parallelogram
Bridge trusses or support beams: these often form parallelograms for strength
Solved examples of parallelograms
Finding area and perimeter
Mika is decorating a placemat shaped like a parallelogram.
It has a base of 10 inches, a side length of 6 inches, and a height of 4 inches.
She needs to determine how much fabric she’ll need to cover the placemat. She also wants to decorate the edge with yarn.
What is the perimeter of the placemat?
Perimeter = 2 × (base + side)
2 × (10 + 6)
2 × 16 = 32 inches
What is the area of the placemat?
Area = base × height
10 × 4 = 40 square inches
Verifying parallelogram properties
To confirm that a shape is a parallelogram, students can look for several key properties. If the shape has any of these, it is a parallelogram:
- Opposite sides are equal
- Opposite sides are parallel
- Opposite angles are equal
- Diagonals bisect each other (cross at midpoint)
Special parallelograms
Connor is building a picture frame for his teacher. The frame is 8 inches long and 5 inches wide.
What is the perimeter of the frame?
Perimeter =2 x (length + width)
2 x (8 + 5)
2 x 13 = 26 inches
What is the area of the frame?
Area = length x width
8 x 5 = 40 square inches
For more examples, head over to Dreambox, an interactive online math program that helps kids practice math concepts through fun games and activities. If your student needs extra geometry support or wants to explore more parallelogram problems, Dreambox is a fantastic learning tool.
FAQs about parallelograms
The four types of parallelograms are: “base” parallelogram, rectangle, rhombus, and square.
To identify a parallelogram, the shape must have at least one of these properties: opposite sides are equal, opposite sides are parallel, opposite angles are equal, diagonals bisect each other.
A parallelogram shape is four-sided, with opposite sides that both run parallel and are equal in length.
A parallelogram is a broader category of shapes that includes rectangles.
