Commutative property
Detailed explanations, real-world examples, and practice with the commutative property to boost your understanding and get ahead in class.
Author
Tess Loucka
Published:
June 2025
Key takeaways
- • The commutative property states that changing the order of values in certain expressions does not alter the result of those expressions.
- • The commutative property only applies to addition and multiplication, not to subtraction or division.
- • The associative and distributive properties also deal with the alteration of expressions.
What is the commutative property in math?
Properties in math are characteristics and rules that can be applied to certain expressions in order to simplify and solve them. Understanding properties can make complicated equations easier, giving you a greater understanding of how math works and improving your solving speed, too.
Today, we’re going to talk about the commutative property and how it functions with the four basic operations: addition, subtraction, multiplication, and division.
Definition of commutative property
So, what is commutative property?
The commutative property says that, when multiplying or adding two values, the order of the values can be swapped without affecting the final result.
Origin of the term "commutative"
To make it easier to remember what the commutative property is, let’s think about the origin of the word “commutative.”
“Commutative” comes from the Latin word “commutativus,” which means “relating to exchange, interchangeable, mutual.” In math, the commutative property states that you can exchange two values in an expression without changing the result.
“Commutative” also contains the root word “commute,” which means “to move or switch,” which directly relates to the idea of swapping numbers around within an expression.
Table of contents
Commutative property of addition
Addition is one example of a commutative operation in math. That’s because, if you have an expression that adds two values together, the order of the two values can change without affecting the result of that expression.
Formula for the commutative property of addition
a + b = b + a
Real-life examples of the commutative property of addition
If you can’t picture how the commutative property of addition works, just imagine two of your favorite fruits sitting on a table in front of you.
In this example, we have one orange and one grape, giving us a total of two fruits. It doesn’t matter if we eat the orange first, then the grape, or eat the grape first, then the orange. Either way, we are eating two fruits!
Visualizing the commutative property of addition
Let’s visualize an example of the commutative property to make this concept easier to understand.
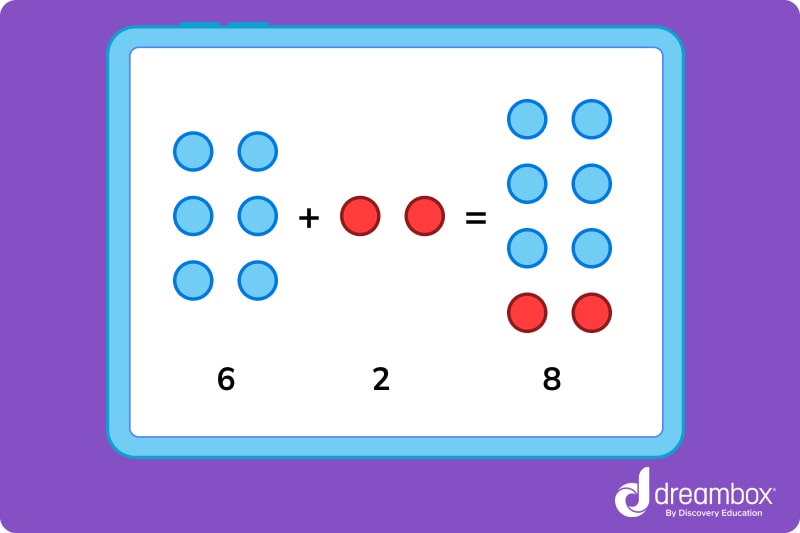
The image above demonstrates that 6 blue dots plus 2 red dots is equal to 8 total dots, while 2 red dots plus 6 blue dots is also equal to 8 total dots.
We can simplify this scenario into the numerical expressions 6 + 2 = 8 and 2 + 6 = 8.
No matter what order 6 and 2 are in, as long as they are being added together, their value will always be 8.
This property, or rule, remains true when adding any values together. In fact, this property applies to adding any number of values together.
10 + 8 + 44 + 0 = 0 + 44 + 8 + 10
Commutative property of multiplication
The commutative property of multiplication says that if two numbers are being multiplied, the order in which you multiply them will not change the result.
Formula for the commutative property of multiplication
a * b = b * a
Practical applications of the commutative property of multiplication
The commutative property of multiplication doesn’t only apply to math problems—you can apply this property to various real-life situations!
Let’s review two examples of the commutative property.
Imagine you are planting seeds in a garden. You have 15 seeds to plant, so you make 15 holes.
From this side of the garden, you might count 5 rows of 3 holes
From this side, you might count 3 rows of 5 holes.
No matter how you look at it, there are always going to be 15 holes in total.
Using numbers, this scenario could be written as 5 * 3 = 3 * 5
Here’s another example:
You have 40 books in your room, and you want to organize them on your bookshelf, which has 8 shelves.
You could organize your 40 books equally onto all 8 shelves by placing 5 books on each shelf.
You could also organize your books by placing 8 books on only 5 shelves.
Either way, all 40 books will be placed on the shelves.
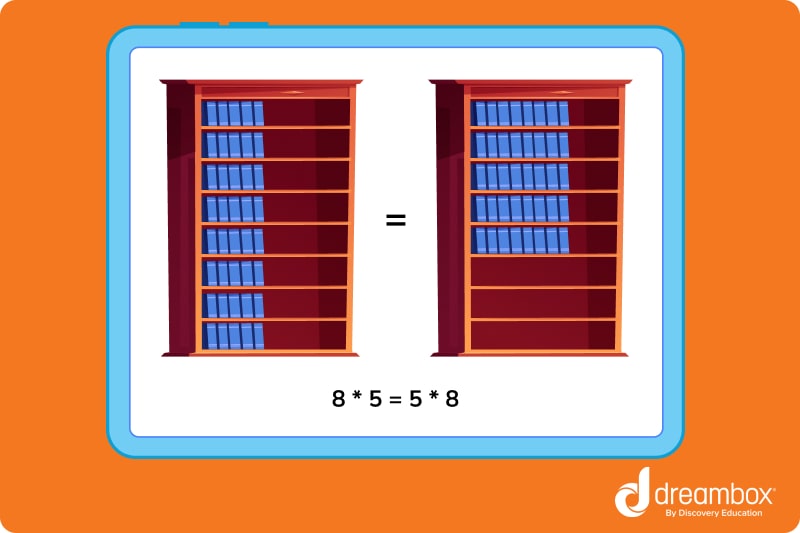
Let’s visualize an example of the commutative property to make this concept easier to understand.
Operations that are not commutative
Not every mathematical operation is commutative. We’ve already reviewed which ones are—addition and multiplication—so let’s move on to the ones that aren’t.
Why subtraction is not commutative
Subtraction is a non-commutative operation because the order of values when subtracting does affect the result.
For instance, 10 – 5 = 5.
If we swapped the values around, we’d get 5 – 10 = -5.
Since 5 does not equal -5, subtraction is not commutative.
Why division is not commutative
Division is the other non-commutative operation in math. Just like subtraction, if you switch the order of values, the result of the expression will change.
8 / 4 = 4
4 / 8 = .5
It is true that 4 does not equal .5. Therefore, division is not commutative.
Understanding the definition of the commutative property is different from knowing how to use it in everyday math. You can be a commutative property expert by completing practice problems and learning more real-world applications.
There are many online math programs and physical resources available to help you on your math journey. So, don’t stop here; keep learning!
How does the commutative property differ from other properties?
The commutative property is often confused with other properties. This is especially true for the associative and distributive properties. But how are they different, and what makes them similar?
Commutative vs. associative property
What the commutative and associative properties have in common is that they work with addition and multiplication only. They also both relate to the order of operations within an expression.
With the commutative property, the ordering of values being added or multiplied does not affect what the final result will be.
With the associative property, changing the grouping of values being added or multiplied in an expression does not change the final result. However, for this to work, the values have to stay in the same order.
That means, (a + b) + c = a + (b + c) and (a * b) * c = a * (b * c).
Let’s test the associative property out!
(4 + 2) + 5 = 6 + 5 = 11
4 + (2 + 5) = 4 + 7 = 11
It is true that 11 = 11. Therefore, addition is an associative operation.
(8 * 3) * 2 = 24 * 2 = 48
8 * (3 * 2) = 8 * 6 = 48
Multiplication is an associative operation because 48 = 48.
Commutative vs. distributive property
Like the commutative property, the distributive property relates to altering expressions without changing their results.
However, the distributive property deals with (you guessed it!) the distribution of values rather than the order of them.
With the distributive property, multiplying two values will always give you the same final result as separately multiplying the addends of one value by the other value.
The formula for the distributive property is a(b + c) = ab + ac.
This may seem confusing at first, but the following example should clear things up:
5 * 12 = 48
To make this expression easier to solve, we can break 12 up into smaller numbers. We’ll choose two numbers that, when added together, equal 12—12 and 2. These are called addends.
Using the distributive property formula, we’ll say a = 5, b = 10, and c = 2.
So, we can rewrite 5 * 12 as 5(10 + 2) = (10 * 5) + (2 * 5) = 50 + 10 = 60.
After breaking 12 into 10 and 2, we were able to individually multiply (or distribute) 5 with these smaller values to get 50 + 10 = 60.
As you can see, this property makes multiplying big numbers a whole lot easier!
Let’s try another example.
Using the distributive property, how could you solve the following expression?
3 * 16 = ?
Try the problem out for yourself, then look at one possible solution below.
In our solution, we decided to split 16 into 10 and 6.
You can split 16 into any combination of addends, such as 15 and 1, 14 and 2, 13 and 3, and so on. The key is to make the problem simpler for you to solve by breaking down large numbers, like 16, into numbers that are easy to work with.
Since 10 and 6 go in the parentheses, we can separately distribute the 3 to them, making (10 * 3) and (6 * 3). We can then add those together to get 48.
Keep in mind that the distributive property only works when the operation within the parentheses is addition or subtraction.
4 * 11 = 44 → 4(5 + 6) = (5 * 4) + (6 * 4) = 20 + 24 = 44.
4 * -1 = 4(5 – 6) = (5 * 4) * (6 * 4) = 20 – 24 = -4
FAQs
An example of the commutative property is 6 + 4 = 4 + 6.
The associative property says you can group numbers in different ways without changing the final result of an expression, while the commutative property says you can change the order of values in an expression without changing the final result.
Commutative and associative are two properties that explain unique mathematical features. The commutative property says that the order of certain values can be changed without altering the result of the expression. The associative property says that the grouping of certain values can be changed without altering the result of the expression.
“Commutative” in math means the moving around of values within an expression. It relates to the word “commute.”
