All About Decagons
Learn all about decagons: how many sides a decagon has, the different types of decagon and be able to answer “what is a decagon” with confidence!
Author
Katie Wickliff
Published:
May 2025
Key takeaways
- • Decagons are a type of polygon that has 10 sides, 10 vertices, and 10 angles.
- • There are several different types of decagons, including regular, irregular, simple, and complex.
- • Students learn mathematical formulas to calculate the area, perimeter, and angles of a decagon.
What is a decagon?
In early elementary geometry, kids focus on basic shapes like circles, squares, and triangles. A few years later, kids are introduced to more complicated shapes, but the focus is still on building a strong foundation in geometry. At this level, kids concentrate on irregular shapes and shapes with multiple parts. They also look closely at shapes with more sides, such as a decagon. In this article, we’ll take a closer look at what a decagon is, highlight its key properties, and explain the different types of decagons. We’ll also share helpful formulas for solving decagon-related problems, which students often encounter in middle school.
A decagon is a type of polygon. It is a flat, closed shape with 10 sides, 10 vertices, and ten angles. There are several types of decagons, each with distinct properties.
Table of contents
Types of decagons: regular, irregular and more
Regular decagon
In a regular decagon shape, all sides are equal in length, and all angles are equal in measure. Each interior angle in a regular decagon measures 144°, and each exterior angle measures 36°. The equal sides and angles make it easier for students to recognize the shape’s pattern, symmetry, and structure.
Irregular decagon
In an irregular decagon, the sides and angles are not all equal. To be considered irregular, at least two of the decagon sides and angles must measure differently from the others.
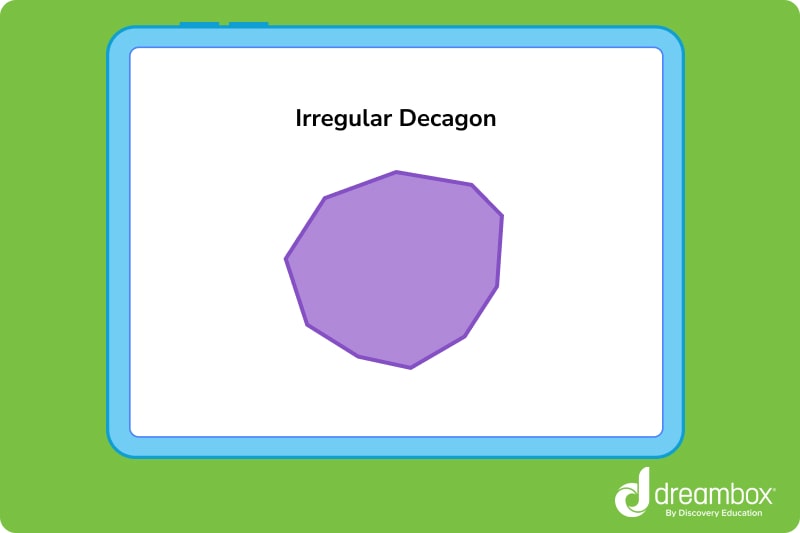
A helpful way to understand the difference between a regular and irregular decagon is to imagine a regular decagon drawn perfectly using a compass or protractor. Every side and angle should be exactly the same. Now, picture a decagon sketched by hand, with variation in the sides and angles. That’s an irregular decagon!
Convex decagon
A convex decagon is a ten-sided shape where all the corners point outward and none of the interior angles are greater than 180°. Instead, a convex decagon bulges outward, giving it a “puffed out” look.
Concave decagon
A concave decagon has at least one side that points inward, forming a “dent.” In this shape, at least one interior angle is greater than 180°. A star is a great example of a concave decagon.
Simple decagon
A simple decagon is flat, clean, and connected from one corner to the next. The sides do not crisscross or overlap. They follow the “rules” of the regular decagons.
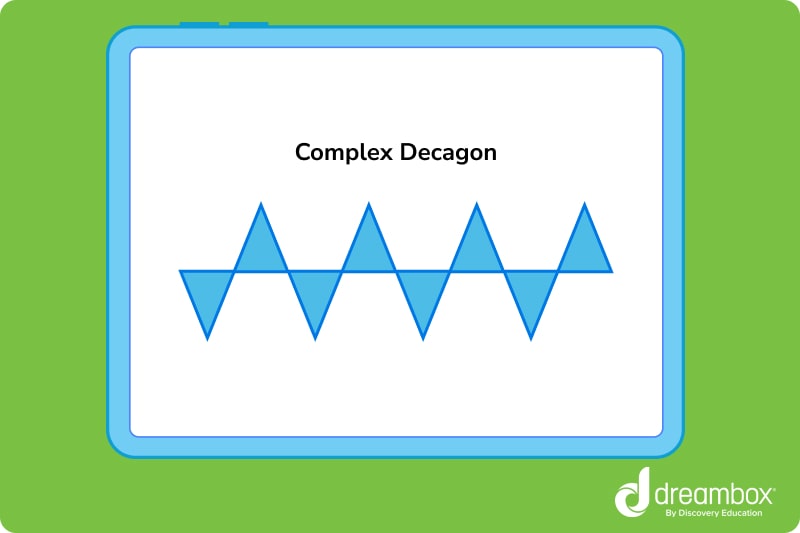
Complex decagon
In a complex decagon, some or all of the sides intersect. Unlike a simple decagon, the shape does not have a smooth outer edge. Most students will begin working with complex decagons in middle or high school.
Key properties of a decagon
Whether a decagon is regular or irregular, they all have several key properties that distinguish them from other shapes.
Number of sides, angles, and vertices
A decagon has 10 sides, 10 angles, and 10 vertices.
Sum of interior angles
The interior angles of a decagon always add up to 1400°.
Sum of exterior angles
The exterior angles of a decagon always add up to 360°.
Number of diagonals
In geometry, a diagonal is a line that connects two non-adjacent corners of a shape. A decagon always has 35 diagonals.
Triangles in a decagon
There are 8 triangles in a decagon, found by dividing the shape into 8 non-overlapping triangles by drawing diagonals to all the other non-adjacent corners.
Decagon formulas: area, perimeter, and angles
Students are usually in middle school before they begin using formulas to calculate the area, perimeter, and angles of a decagon.
Perimeter of a decagon
To calculate the perimeter of a decagon, simply add up the lengths of all 10 sides. If the decagon is regular, students can multiply one side by 10:
Perimeter = 10 × side length
This is the first decagon formula students generally learn, usually in upper elementary school.
Interior and exterior angle formulas
Interior Angle Formula
- To find the total of all the interior angles in any polygon, use this formula:
Sum of interior angles= (b-2) x 180°
b= the number of sides
So for a decagon, the formula is:
(10-2) x 180°= 8 x 180°
8 x 180°=1440°
Then, divide the sum of the interior angles (1440°) by 10 to find the total of an individual angle in a regular decagon:
1440° / 10 = 144° per interior angle
Exterior Angle Formula
- The sum of all the exterior angles in any polygon is 360°
So, to find the total of all the exterior angles in a regular decagon:
360° / 10 = 36° per exterior angle
Another way for your student to calculate the exterior angle is by knowing that all interior angles and their exterior angle make a straight line, which is always 180°.
So if they know that one interior angle is 124°, the exterior angle is:
180° – 124° = 56°
Area of a decagon
Students usually don’t begin learning how to calculate the area of a decagon until late middle school or early high school. These complex formulas require an understanding of pi and the ability to use calculators effectively.
Here is the formula to find the area of a decagon:
Area=25×side length 2 ×cot(10π)
Real-world examples of decagons
While decagons are harder to spot outside the classroom as more common shapes like circles or squares, there are still several ways to help your student notice different types of polygons. For example, while a stop sign has 8 sides (octagon), it can help kids better visualize what a 10-sided shape might look like. True decagons are more likely to appear in decorative designs, such as floor tiles, wall art, or even playground patterns.
Although they are not as common today, some countries have decagon-shaped coins. These unique designs help people, specifically those with visual impairments, tell the coins apart by touch. Decagonal coins are also sometimes made to commemorate special events or cultural traditions.
Why decagons matter in geometry
Decagons play an important role in helping students understand geometry. When working with decagons, students learn to recognize patterns in shapes and angles, apply mathematical formulas, and identify and compare different types of polygons. Studying decagons also familiarizes students with important geometry terms, such as interior angles, vertices, and symmetry.
Kids can practice identifying decagons and other polygons through hands-on activities, such as using pattern blocks or popsicle sticks to build the shape and explore its properties. For even more practice, check out Dreambox, an interactive math program that helps kids build math skills through engaging activities and lessons. Whether your child needs additional support or an extra challenge, Dreambox adapts in real time to create a personalized experience.
Exploring more polygons
In addition to decagons, students will explore a variety of polygons as they move through elementary school, middle school, and high school. Some of these polygons include:
- Pentagons: 5 straight sides and 5 angles
- Hexagons: 6 straight sides and 6 angles
- Octagons: 8 straight sides and 8 angles
- Nonogons: 9 straight sides and 9 angles
FAQs about decagons
A decagon has 10 sides.
Yes, a decagon shape has ten sides.
A decagon is a type of polygon. It is a flat, closed shape with ten sides, ten vertices, and ten angles.
A real life example of a decagon is the 50 cent coin from Belize.
A shape with 9 sides is not a decagon, because a decagon always has 10 sides. A shape with 9 sides is called a nonagon.
